试题:
(本题满分13分)如图,分别过椭圆 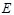 : :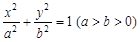 左右焦点 左右焦点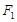 、 、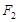 的动直线 的动直线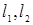 相交于 相交于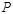 点,与椭圆 点,与椭圆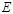 分别交于 分别交于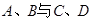 不同四点,直线 不同四点,直线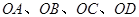 的斜率 的斜率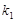 、 、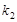 、 、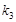 、 、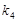 满足 满足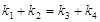 .已知当 .已知当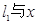 轴重合时, 轴重合时,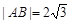 , ,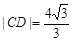 . .(1)求椭圆 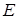 的方程; 的方程;(2)是否存在定点 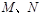 ,使得 ,使得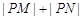 为定值.若存在,求出 为定值.若存在,求出 点坐标并求出此定值,若不存在,说明理由. 点坐标并求出此定值,若不存在,说明理由.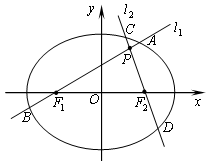 |
圆锥曲线综合
2016-05-26
答案:
我来补答展开全文阅读



 (2)M、N坐标分别为
(2)M、N坐标分别为 ;
;
 ,|CD|=
,|CD|= ,由此能求出椭圆E的方程.
,由此能求出椭圆E的方程. ,得(2+3m12)x2+6m12x+3m12−6=0,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|为定值2
,得(2+3m12)x2+6m12x+3m12−6=0,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|为定值2 .
. ,即
,即 , 2分
, 2分 ,
, ,(4分)
,(4分) ,
, , ∴椭圆E的方程为
, ∴椭圆E的方程为 ,
, ,设
,设 ,
, ,
, 得:
得: ,
, ,
, .(7分)
.(7分)
 ,
,
 . 9分
. 9分 ,∴
,∴ ,即
,即 .
. , ∴
, ∴ .
. ,则
,则 ,即
,即 , 11分
, 11分 上, 12分
上, 12分